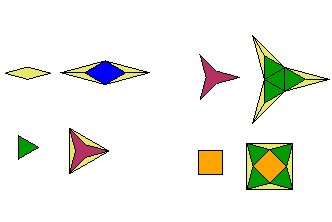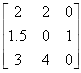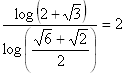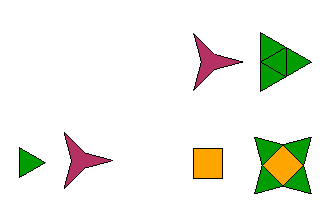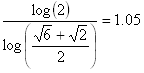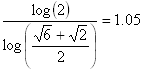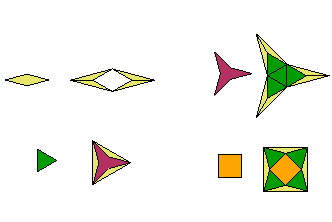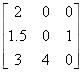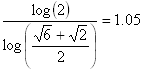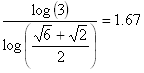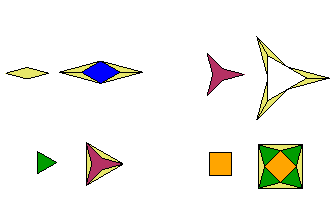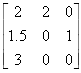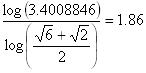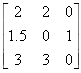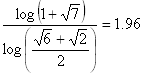Fractal Dimension

For a fractal that tiles with a single shape (such as the Sierpinski gasket or the Menger sponge), the fractal dimension is found using the following formula.

In other words, as the pieces are scaled by a factor 1/scaling_factorⁿ, the number of pieces needed to tile the design is number_of_piecesⁿ. Then the fractal dimension is found by the equation above.

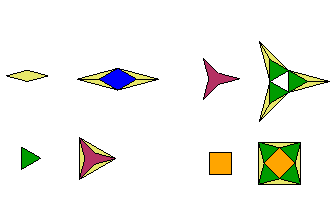
In the pictures on this site, the tiling uses multiple shapes. However, the number of pieces is dominated by the largest eigenvalue eⁿ, so the formula can still be applied to the tilings on this site.

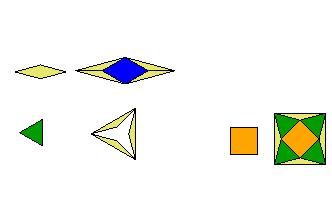
The following table summarizes the fractal dimension of some of the designs on this site. (Note that the first design, the solid square, is not a fractal.)

Fractal	Substitution Tiling	Substitution Matrix	Equation for eigenvalues	Fractal Dimension
			x³-2x²-7x+2=0, solutions are , , and -2
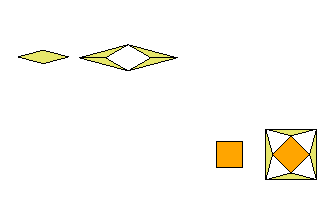
		(note that diamonds are not included)	x²-4=0, solutions are 2 and -2
		(note that triangles and y-shaped stars are not included)	x-2=0, solution is 2
			(2-x)(x²-4)=0, solutions are -2, 2, and 2. Double root at 2 means grows as n2ⁿ
		(note that y-shaped stars are not included)	x²-2x-3=0, solutions are 3 and -1.
			x³-2x²-3x-6=0, see Note 1 for solution.
			x³-2x²-6x=0, solutions are 0, ,

Note 1: Mathcad gives the exact formula for the real solution as

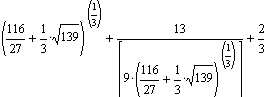
which is roughly 3.4008846

Back to Mathematics behind the Designs.