The first set of designs is based on the following substitution tiling without any holes. So while these are not fractals, they are still interesting designs.
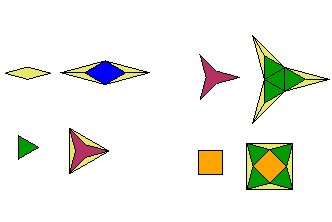
The first pictures show the diamonds D0 to D6, triangles T0 to T6, and Y-shaped stars Y0 to Y6.
|
PDF version (72 KB) |
|
|
PDF version (63 KB) |
|
|
PDF version (122 KB) |
The next pictures show squares S0 to S6 and S7.
|
PDF version (139 KB) |
|
|
PDF version (426 KB) |
If you look at the pictures, it appears that wheels or circles emerge in the design that become more and more complex. This happens whenever 12 diamonds come together at a point, which will happen at every vertex because of the nature of the transformation. The following diagram shows how 12 diamonds grow in the shape of a wheel, W0 to W4 and W5.
|
PDF version (110 KB) |
|
|
PDF version (297 KB) |
Other shapes can be transformed, too. The following pictures show a dodecagon and dodecagram growing. (Notice these look very similar to the 12 diamonds above.)
|
PDF version (108 KB) |
|
|
PDF version (59 KB) |
The following shows one possible way for a hexagon to grow.
|
PDF version (97 KB) |
The next picture shows a hexagon and hexagram growing, using each other in the process of growing. Notice that the hexagon pattern that emerges is quite different from the one above.
|
PDF version (96 KB) |
|
|
PDF version (82 KB) |
Copyright 1998-2004 by Jim Millar











