Square-Triangle Tilings

Introduction

The discussion below presents an introduction to square-triangle tilings shown in the gallery on this site.

Basic blocks for substitution tiling

There are multiple possible ways for the square to inflate. The following diagram shows the possible inflation rules for squares.

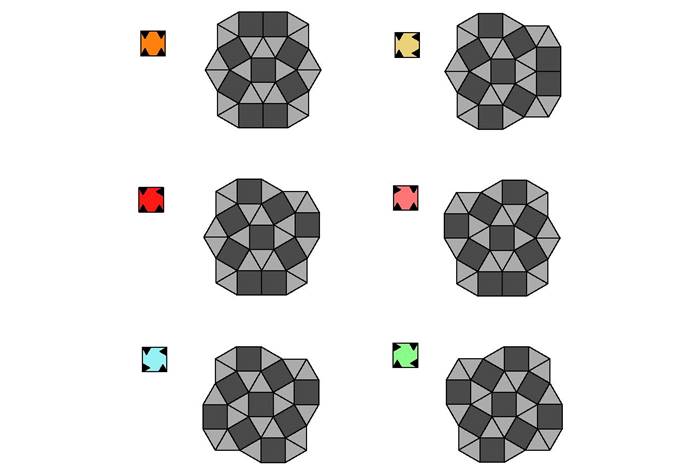
· The squares in the first row are labeled H and T, because the symmetry of the squares is reflected in the corresponding label.

· The squares in the second row are labeled R and F. The lack of symmetry in the tilings is similar to the lack of symmetry of the letters. For a reflectively symmetric inflation rule I consider these to be the same square, since tiling one of them determines the tiling of the other.

· The squares in the third row are labeled Z and S. Similar to the tilings, these letters are only rotationally symmetric (unfortunately not 90 degree like the tilings, but it’s what it is.) For the reflectively symmetric inflation rule I consider these to be the same square.

Similarly, there are multiple ways for the triangle to inflate, shown in the following diagram.

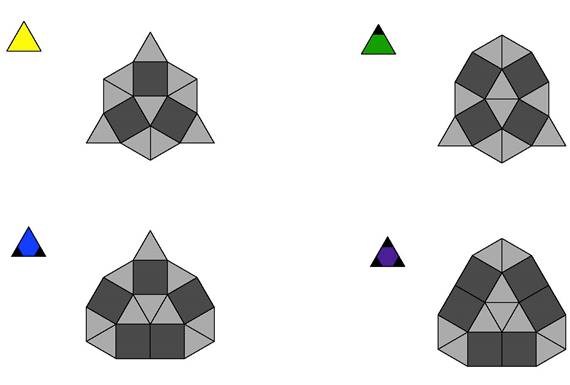
· The first row has triangles I label Y and G (for their color).

· Likewise the second row has triangles I label B and P.

As each gray square and triangle can be any of the 6 squares or 4 triangles, there are many possible square-triangle tilings. The one constraint for all tilings is that they need to follow the matching rules, described below. For the tilings on this site, I have selected the same coloring of squares and triangles. (I have intentionally made the R and F colors similar, since I consider these to be the same tile with reflectively symmetric tiling. Similarly, I intentionally made the Z and S colors similar.)

Stylistically, I like leaving the edges that overlap. Some will have half-triangles and half-squares to show an exact inflation. Others will have half of the edge with the whole triangle and square, leaving holes on the other half of the edge for the mating shape. This allows for exact tiling, but in my opinion the resulting diagrams don’t show the reflective symmetry very well.

Matching Rules

There are three types of edges (all three exhibit on the tan T square at the top right of the first diagram). They are

· Edge with 2 squares and 2 triangles

· Edge with 1 square and 2 triangles

· Edge with 0 squares and 2 triangles

Squares and triangles are adjacent in a tiling only if their inflation rules match in the overlap of the squares and triangles that stick out.

Matching rules formalize this a bit by putting marks on the edges where the square sticks out in the inflation rule. Each edge has 0, 1, or 2 marks (all 3 types are seen in the tan T square above). Match rules enforce edge matches when selecting squares and triangles to populate the inflation rules. Squares and triangles are only adjacent in a tiling when their edge matching rules match. This means the inflated tiling will have the correct overlaps.

Some examples

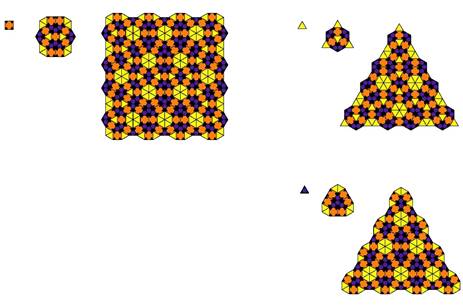
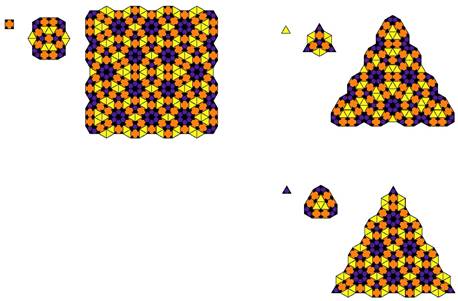
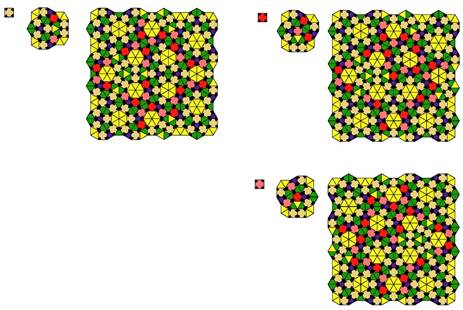
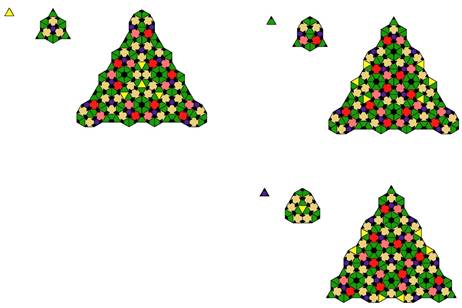
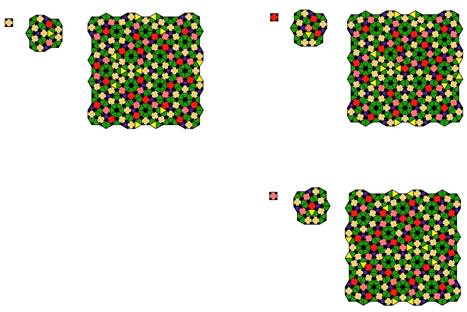
The first two tilings below show square-triangle tilings utilizing only one type of square (tiling 2 and tiling 3 in the gallery).

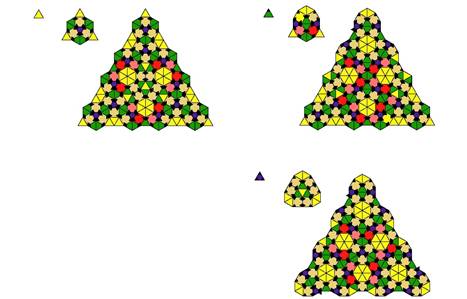
The next two tilings below show a tiling with 2 types of square, attributed to Martin Schlottmann (tilings 5 and 6 in the gallery).

Tiling 5:

Tiling 6:

Types of Vertices

The following diagram shows 3 types of vertices, and the 2 possible matching rules for each type of vertex.

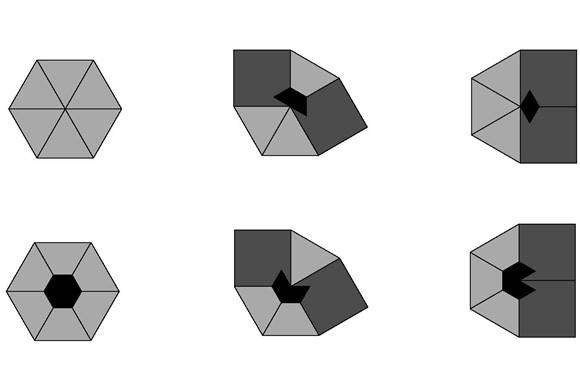
· 6 triangle

· 3 triangle and 2 squares not next to each other

· 3 triangle and 2 square next to each other

4 squares do not appear together in any tiling.

Complementary tilings

The two tilings 2 and 3 are related to each other in the following way: If you take tiling 2 and change the marking of every vertex to be its opposite, per the diagram above, you get tiling 3. In this sense they are complementary.

Similar tilings

The two tilings 5 and 6 are related to each other in the following way: if you take tiling 5 and change only the marking at the corners of the inflation rule of every tile, you get tiling 6. The inflation rule of tiling 5 has a yellow triangle with no mark at the corner of the inflation rules. Tiling 6 has a green triangle with a mark at the corner of the inflation rules. The rest of the inflation rules for the triangles and squares is the same between the two tilings. However, the second level inflation of each looks quite different from each other. Tiling 5 is attributed to Martin Schlottmann, but since tiling 6 is similar only to a trivial difference, I attribute both to Martin Schlottmann throughout the site.

In the gallery I group tilings together that are complementary and similar to each other.

Mandalas

A beautiful feature of the tilings is the behavior at vertices with repeated inflation. Because every inflation rule has triangles at the corner, every vertex in a tiling will have 6 triangles at the next inflation level. In looking at the sets of 6 triangles that manifest in an inflation, there are fixed and periodic points.

· In many cases, a pattern of 6 triangles has an inflation with the same 6 triangles at the center. The vertex where these 6 meet is a fixed point.

· In some cases, a pattern of 6 triangles has an inflation with a different set of 6 at the center, and this second set of triangles has an inflation with the first set of 6 at the center. The vertices at the center of these sets of 6 triangles are periodic points with period 2.

In the gallery of square-triangle tilings, I have not found periodic points with period greater than 2.

The mandalas in the gallery document all of the fixed and periodic points in the various tilings.

The tilings on this site

The tilings on this site are square-triangle tilings with both rotational and reflective symmetry (specifically with the following constraints):

· Any tile must match any other tile when the matching rules match (e.g. on an edge with a single square, the same colored square is used on all tiles such that inflated tiles match)

· One substitution rule for any colored tile

· Substitution rule demonstrates corresponding rotational symmetry

· Substitution rule demonstrates corresponding reflective symmetry

If you include tilings with 3 or 4 squares in the inflation rules, I estimate around 32,000 tilings are possible that are reflectively symmetric.

The tilings on this site are all the square-triangle tilings I could find that use only 1 or 2 of the 4 squares.

Back to Gallery of Square-Triangle Tilings