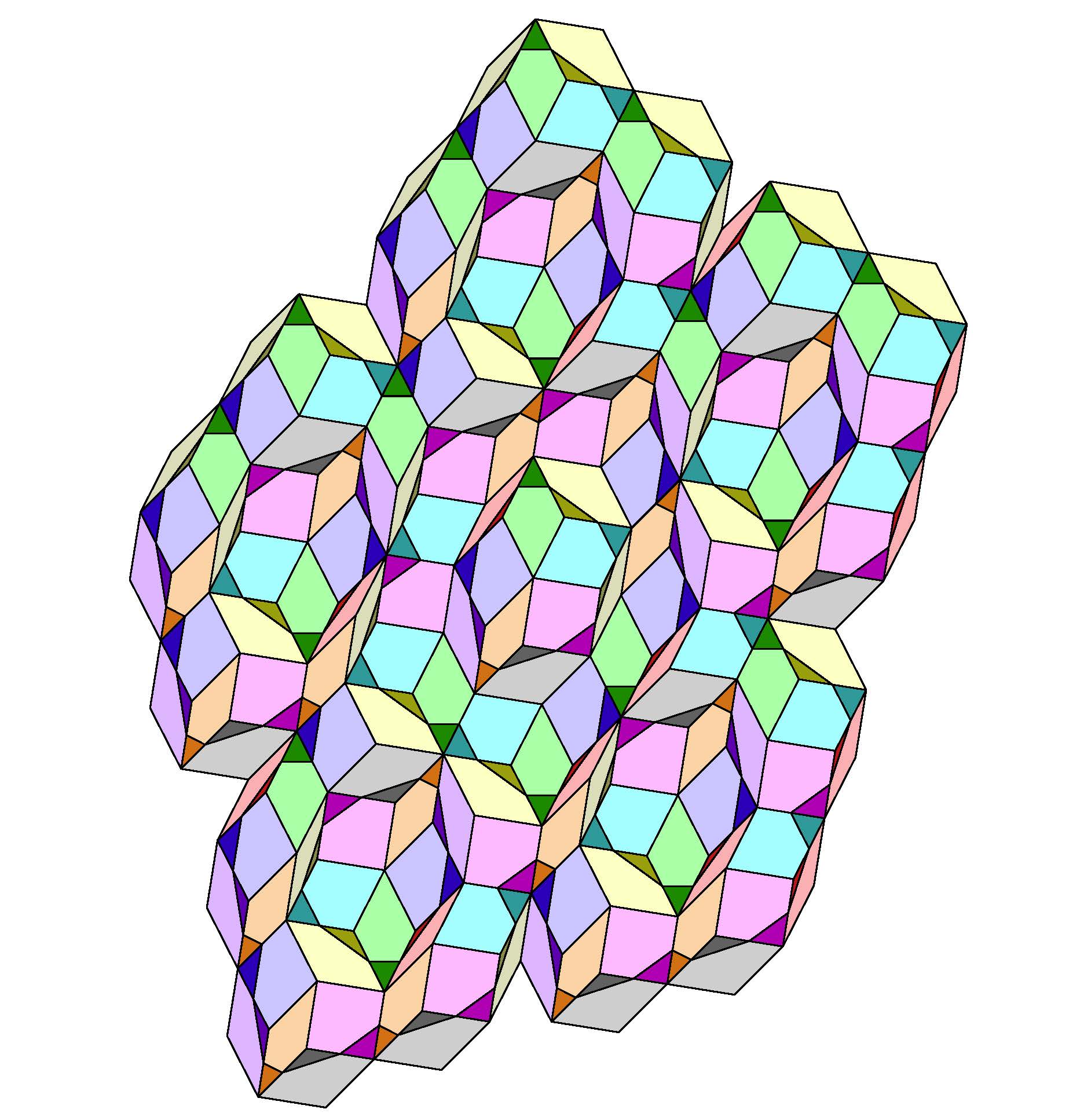
Generalized Penrose
tiling
The following set of pieces show how the Penrose tiling has three degrees of freedom.
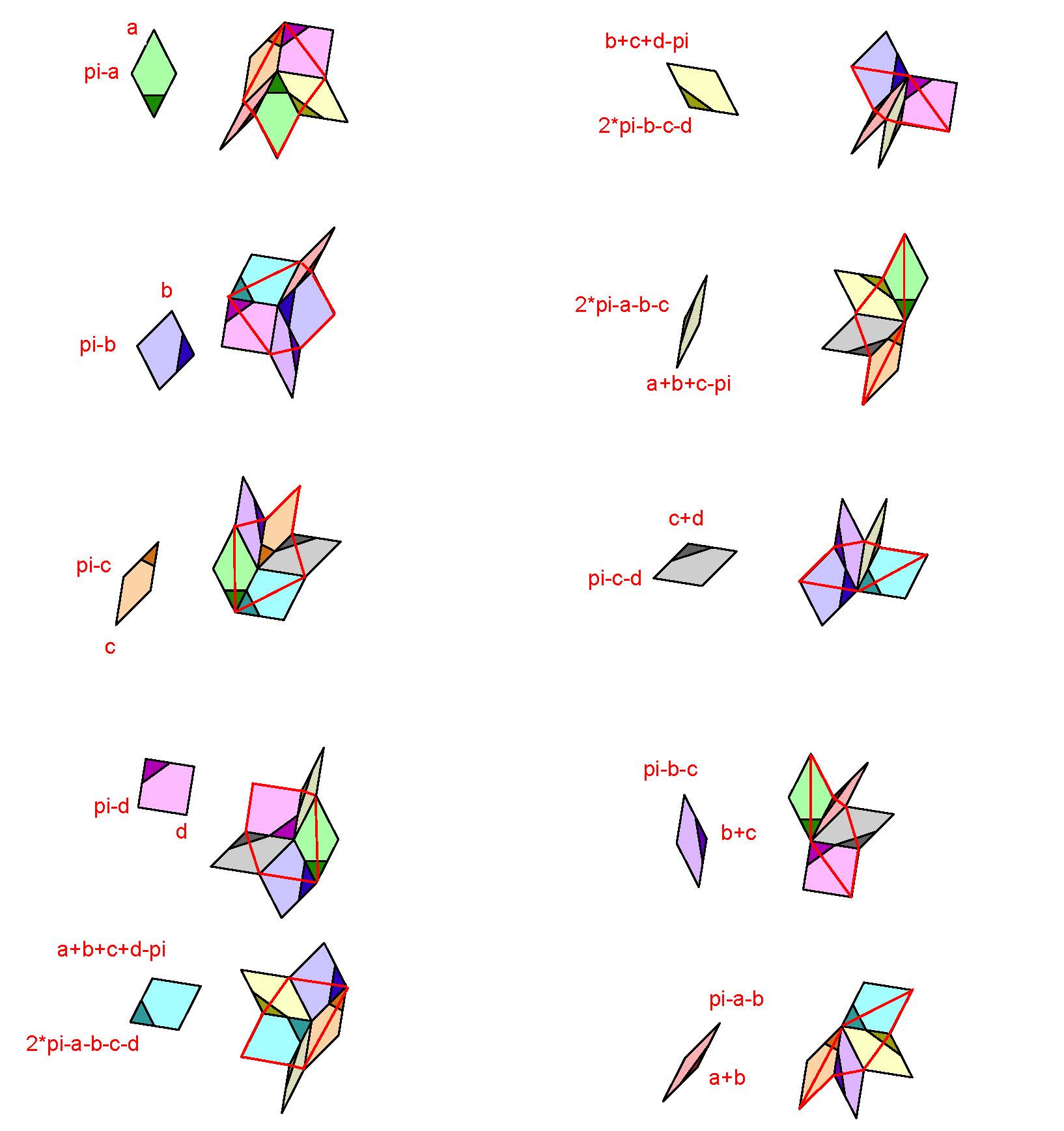
This shows the transformation rule for a Penrose tiling using arbitrary rhombs, all sides unit length, with 4 degrees of freedom in arbitrary angles a, b, c, and d all >0, and a+b<pi, b+c<pi, c+d<pi, a+b+c>pi, and b+c+d>pi. The designs rotate but cannot flip over. The 5 on the left are the Penrose fat rhombs, and the 5 on the right are the Penrose thin rhombs..
Originally posted at pinterest.
The first place I saw the substitution tiling for the Penrose tiling was in Matching Rules and Substitution Tilings page 61 by Chaim Goodman-Strauss.
Return to other ideas for designs.
Copyright 2015-2016 by Jim Millar