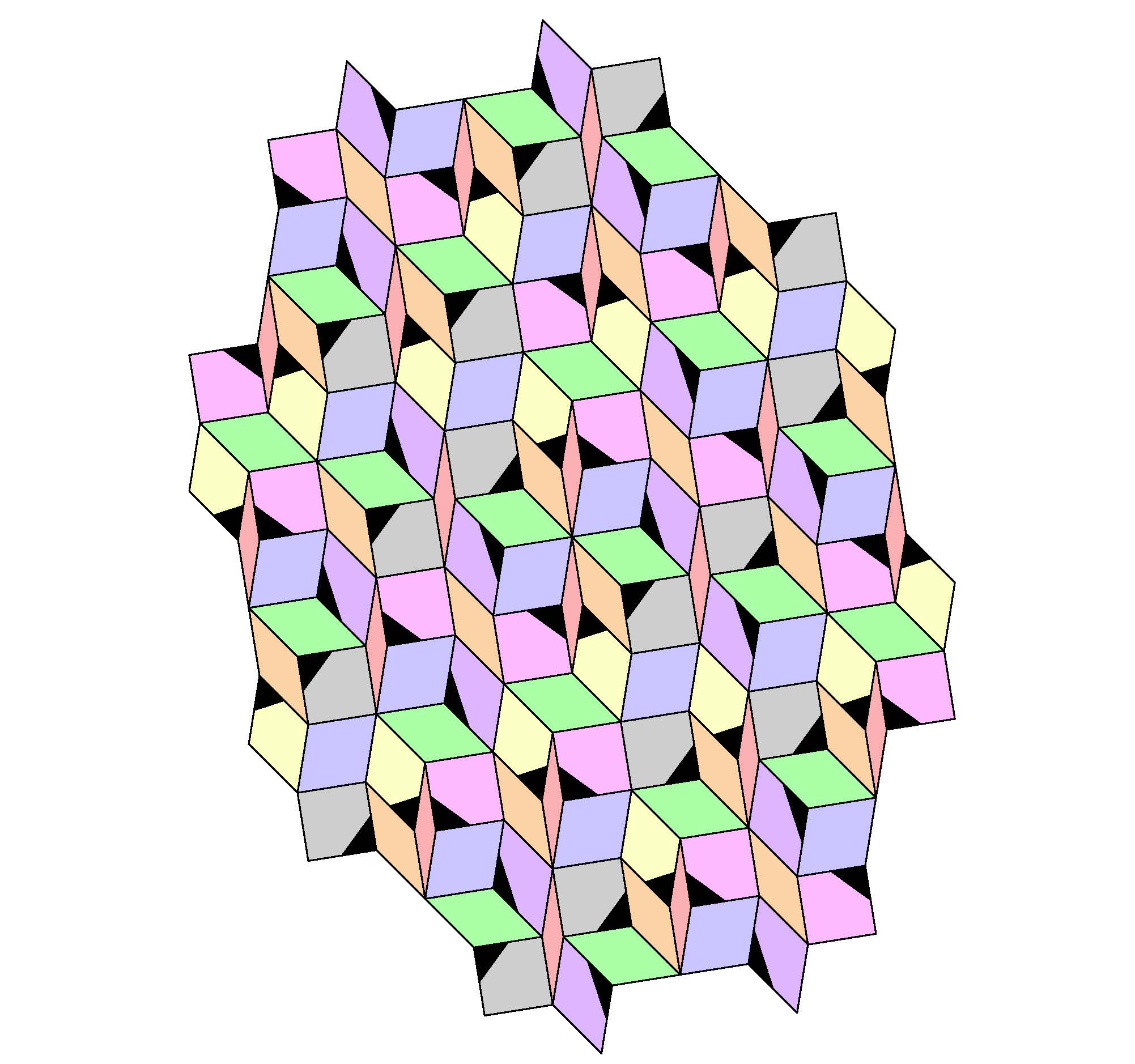
Generalized Ammann tiling
The following set of pieces show how the Ammann tiling has three degrees of freedom.
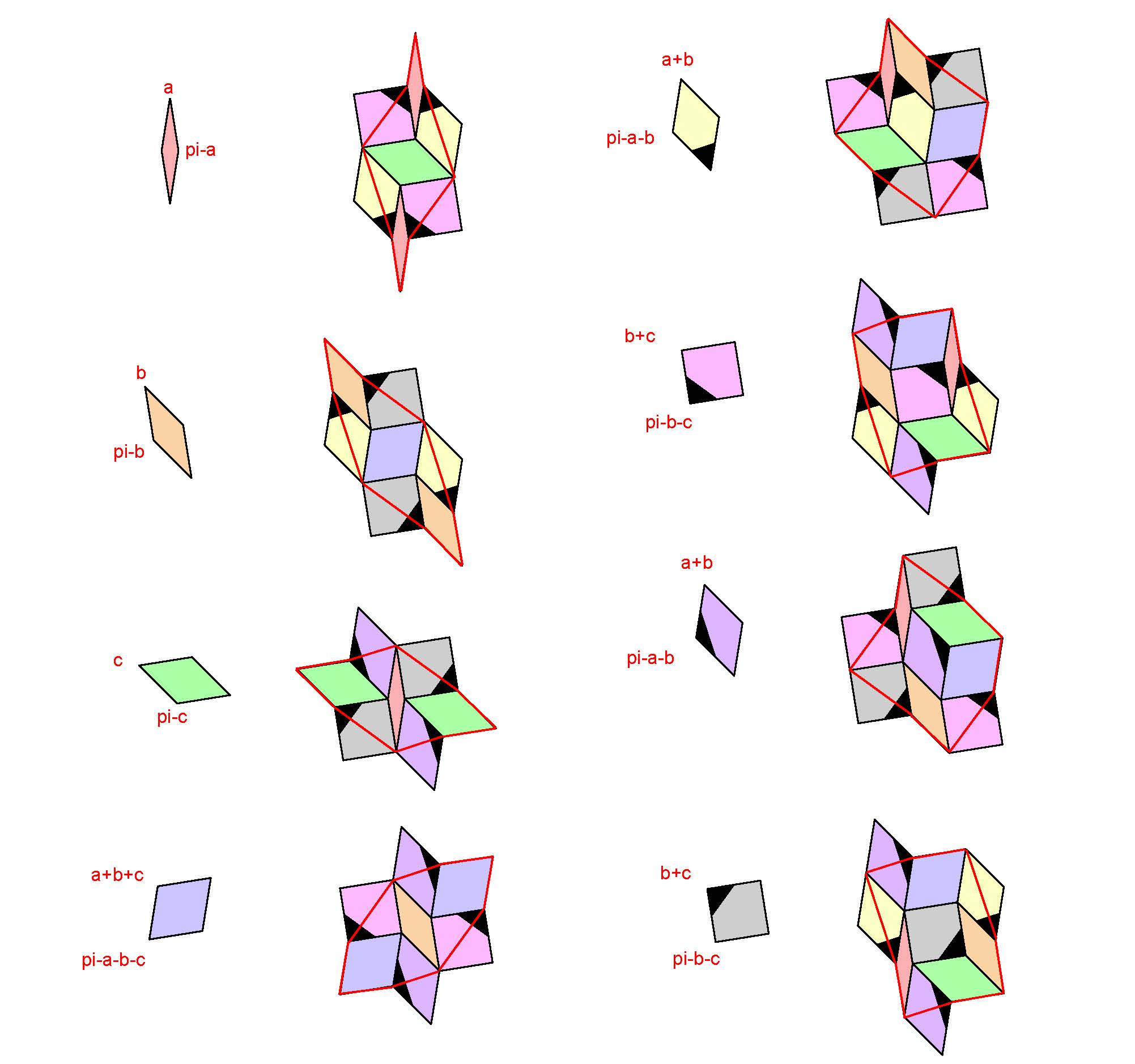
This shows the transformation rule for an Ammann tiling using arbitrary rhombs, all sides unit length, with 3 degrees of freedom in arbitrary angles a, b, and c all >0, and d=pi-a-b-c. The designs rotate but cannot flip over (so the black-tipped pieces have no symmetry).
If a=b=c, then the b tile expands with straight edges. If b=2*pi/k for integer k, this tile rotates k-fold around a vertex to produce a k-fold tiling of the plane, for any integer k.
Originally posted at pinterest.
Return to other ideas for designs.
Copyright 2015-2016 by Jim Millar